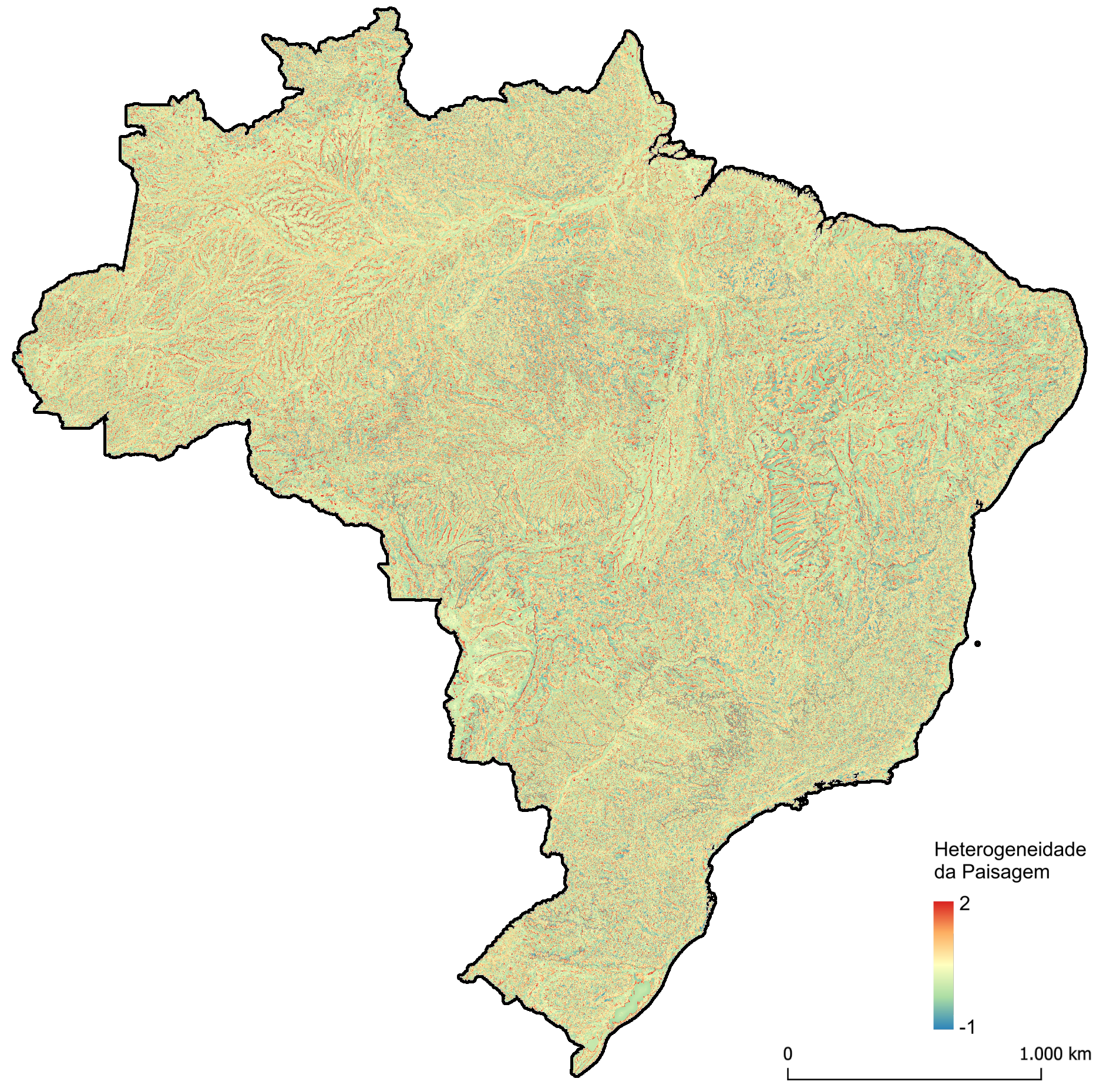
11 Heterogeneidade da paisagem
A heterogeneidade da paisagem, considerada no nosso estudo, é uma métrica composta relacionada à diversidade de microclimas presentes em uma determinada localidade. Essa métrica é calculada através de médias hierárquicas de valores de Z de quatro variáveis distintas: variedade de formas de relevo, amplitude altitudinal, índice de áreas úmidas e riqueza de solos. A seguir, descreveremos como cada variável que compõe a métrica é criada e como elas são combinadas para formar a heterogeneidade da paisagem.
11.1 Bases de dados utilizadas
Utilizamos o modelo digital de elevação (DEM) do Merit-DEM (Yamazaki et al., 2017), na resolução espacial de 90 m, como base para os cálculos de terreno como declividade, exposição do relevo e índice de posição topográfica (TPI). Esse DEM é um produto em escala global, permitindo a replicabilidade das análises em outras regiões, e possui correções de vários vieses derivados de imagens de radar, principalmente em áreas com alta densidade de florestas como a floresta Amazônica. Essas correções têm o propósito de transformar os dados de um modelo digital de superfície (que considera os objetos acima do terreno) em um modelo digital de terreno (que considera a elevação ao nível do solo).
Além disso, o Merit-DEM já possui uma camada de acúmulo de fluxo, em escala global, disponível no Merit-Hydro (Yamazaki et al., 2019). Essa camada de acúmulo de fluxo possui correções para áreas planas e para o efeito da densidade de árvores no cálculo da rede hidrográfica (Yamazaki et al., 2019), que são importantes para a análise de florestas tropicais com alta densidade de árvores. Entretanto, o acúmulo de fluxo não captura adequadamente a distribuição e área de lagos e rios largos, como o rio Amazonas. Desta forma, nós incluímos a classe 33 do MapBiomas Coleção 8 (MapBiomas Project, 2023), que representa os rios e lagos, para complementar as informações sobre as áreas úmidas. O MapBiomas é um projeto nacional de mapeamento e classificação de mudanças do uso do solo dos últimos 37 anos (1985 a 2022), a partir de dados de sensoriamento remoto.
11.2 Variáveis que compõem a heterogeneidade da paisagem
Variedade de formas de relevo (landforms)
As formas de relevo representam a variação na umidade, exposição à radiação solar, velocidade de ventos e deposição de sedimentos na paisagem (Anderson et al., 2016; Dobrowski, 2011). Essa classificação é determinada pelas variáveis de declividade do relevo (slope), exposição do relevo (aspect), índice de posição topográfica (topographic position index), índice de umidade (moisture index) e distribuição de rios e lagos. A combinação dessas variáveis permite identificar os topos de montanhas e vales, áreas íngremes ou planas, exposição do relevo com mais sombra ou incidência solar, áreas secas ou úmidas dado o acúmulo de fluxo, declividade do relevo e a presença de lagos e rios (Figura 11.1). A classificação foi baseada em estudos anteriores (Anderson et al., 2012, 2014, 2016, 2023; Fels & Matson, 1996) conduzidos para a América do Norte (https://crcs.tnc.org/pages/land). A variedade do relevo é representada aqui pela quantidade de formas de relevo dentro de uma vizinhança da célula focal (pixels). Primeiro, classificamos as formas de relevo e contabilizamos a quantidade delas no entorno de cada célula.
A análise conduzida no presente estudo apresentou algumas modificações com relação aos estudos anteriores. Para o cálculo da posição topográfica foi substituído o landscape position index (LPI; Anderson et al. (2012)) pelo topographic position index (Weiss, 2001). Além disso, a exposição do relevo (faces quentes ou frias) foi ajustada para o hemisfério sul. Por fim, a classificação das formas de relevo foi ajustada para valores de TPI e índice de umidade que melhor classificavam as formas de relevo das paisagens analisadas.
Declividade do relevo (slope)
A declividade do relevo foi calculada pela função ee.Terrain.slope, como um gradiente local das 4 células adjacentes. Os resultados são apresentados em graus de declividade (0º a 90º).
Exposição do relevo (aspect)
A exposição do relevo foi calculada pela função ee.Terrain.aspect, como um gradiente local das 4 células adjacentes. Os resultados são apresentados em graus da direção do relevo (0º = norte, 90º = leste, 180º = sul e 270º = oeste). Nós dividimos a exposição do relevo em dois grupos, baseados na quantidade de incidência solar, sendo células com valores entre 90º e 270º classificadas como faces frias e aquelas com valores entre 0º a 90º e 270º a 360º, classificadas como faces quentes.
Índice de posição topográfica (TPI)
O cálculo do TPI foi feito em três escalas com uma janela circular com 7, 11 e 15 células de raio. Ele foi calculado a partir da soma da diferença da elevação da célula focal para as suas vizinhas (\(i\)), dividida pelo número de células vizinhas (\(n\)).
\[ TPI = \frac {\sum _{i}^{n}\left(vizinhança_i - focal \right)}{n} \]
O índice é composto pela média de TPI das três escalas, o que permite a consideração de níveis locais e regional de resolução da paisagem (Theobald et al., 2015). Essa abordagem foi implementada para permitir a classificação de formas de relevo que emergem tanto em escalas locais (ex. vales e topos de montanhas), quanto regionais (ex. topos planos de chapadas; (Fels & Matson, 1996)). Os tamanhos das janelas foram ajustados visualmente para que representassem as formas de relevo.
O índice é composto pela média de TPI das três escalas, o que permite a consideração de níveis locais e regional de resolução da paisagem (Theobald et al., 2015). Essa abordagem foi implementada para permitir a classificação de formas de relevo que emergem tanto em escalas locais (ex. vales, topos de montanhas) quanto regionais (ex. topos planos de chapadas; Fels & Matson (1996)). Os tamanhos das janelas foram ajustados visualmente para que representassem as formas de relevo.
Índice de umidade (moisture index)
O índice de umidade (moisture index) foi calculado com base no acúmulo de fluxo, gerado a partir do Merit-Hydro, e na declividade do relevo, calculadas anteriormente.
\[ moisture.index = \frac{\log \left(fluxo+1\right)}{\left(slope+1\right)} \times1000 \]
Após o cálculo do índice de umidade para cada célula, suavizamos o padrão de distribuição da rede de drenagem como a média do índice dentro de uma janela circular com uma célula de raio.
Transformando os índices em classes
Cada índice (declividade e exposição do relevo, TPI e índice de umidade) foi transformado em classes para formar os tipos de formas de relevo. A declividade e exposição do relevo seguiram a classificação em Anderson et al. (2016), com a exposição do relevo ajustada para o Hemisfério Sul. Os ajustes dos limiares de TPI e índice de umidade foram definidos visualmente. Classificamos como áreas úmidas somente células com índice de umidade acima de 3.000, uma vez que valores menores superestimavam a distribuição de corpos d’água em áreas planas. Por fim, combinamos o mapa de áreas úmidas com o de água e lagos do MapBiomas.
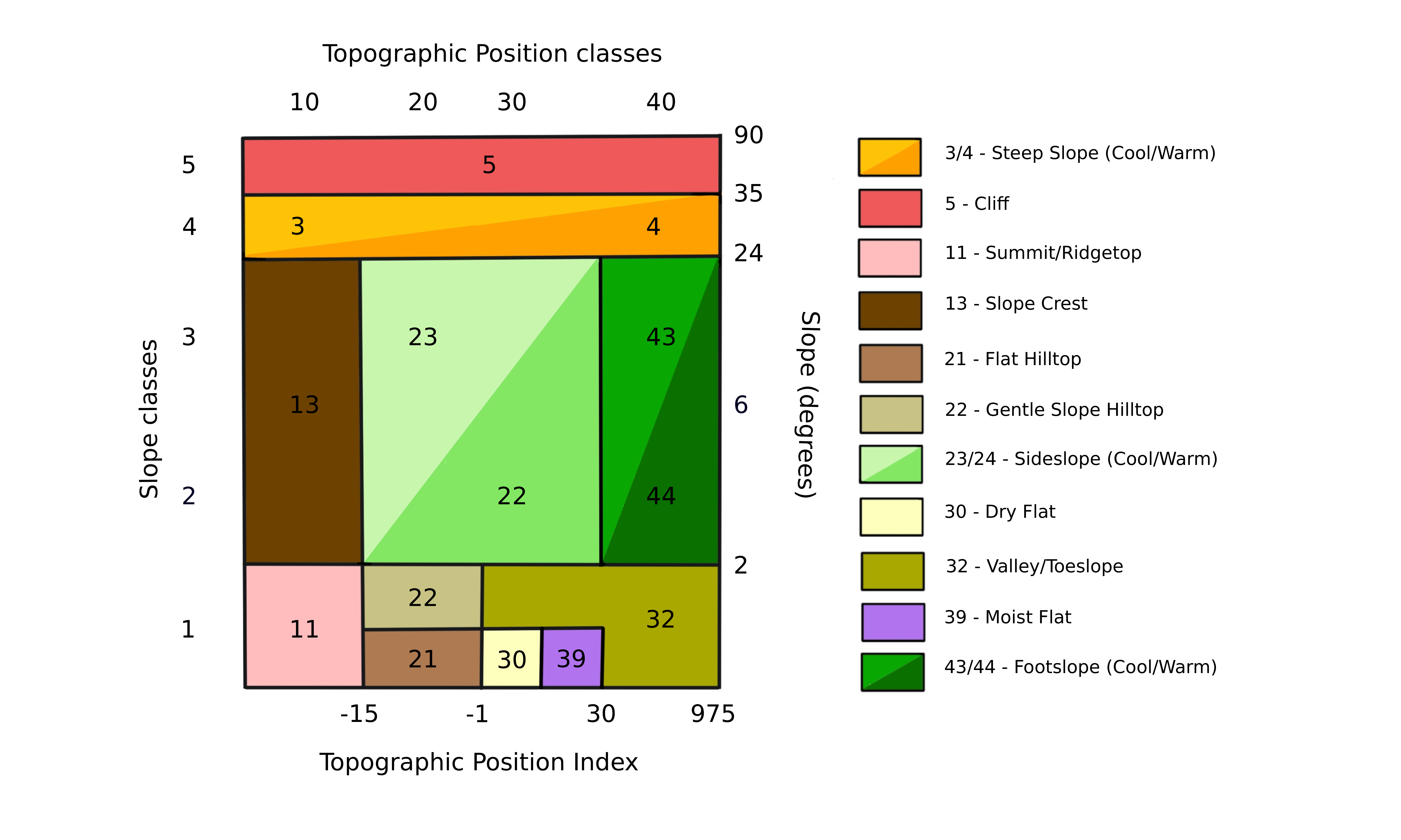
Combinando as variáveis e classificando as formas de relevo
As classes de cada variável foram combinadas para representar as formas de relevo como um código numérico (Figura 11.2): índice de umidade * 1000; exposição do relevo * 100; TPI * 10; declividade do relevo * 1. Por exemplo, o código 11 (0011) representa a primeira classe de declividade (áreas de baixa declividade) e a primeira classe de TPI (posição do relevo mais alta que o entorno), sendo, portanto, um topo de montanha (summit). No entanto, alguns códigos tiveram que ser inspecionados visualmente para classificar apropriadamente alguns tipos de formas de relevo, como por exemplo encostas (sideslopes), vales (valleys) e sopés (toeslopes).
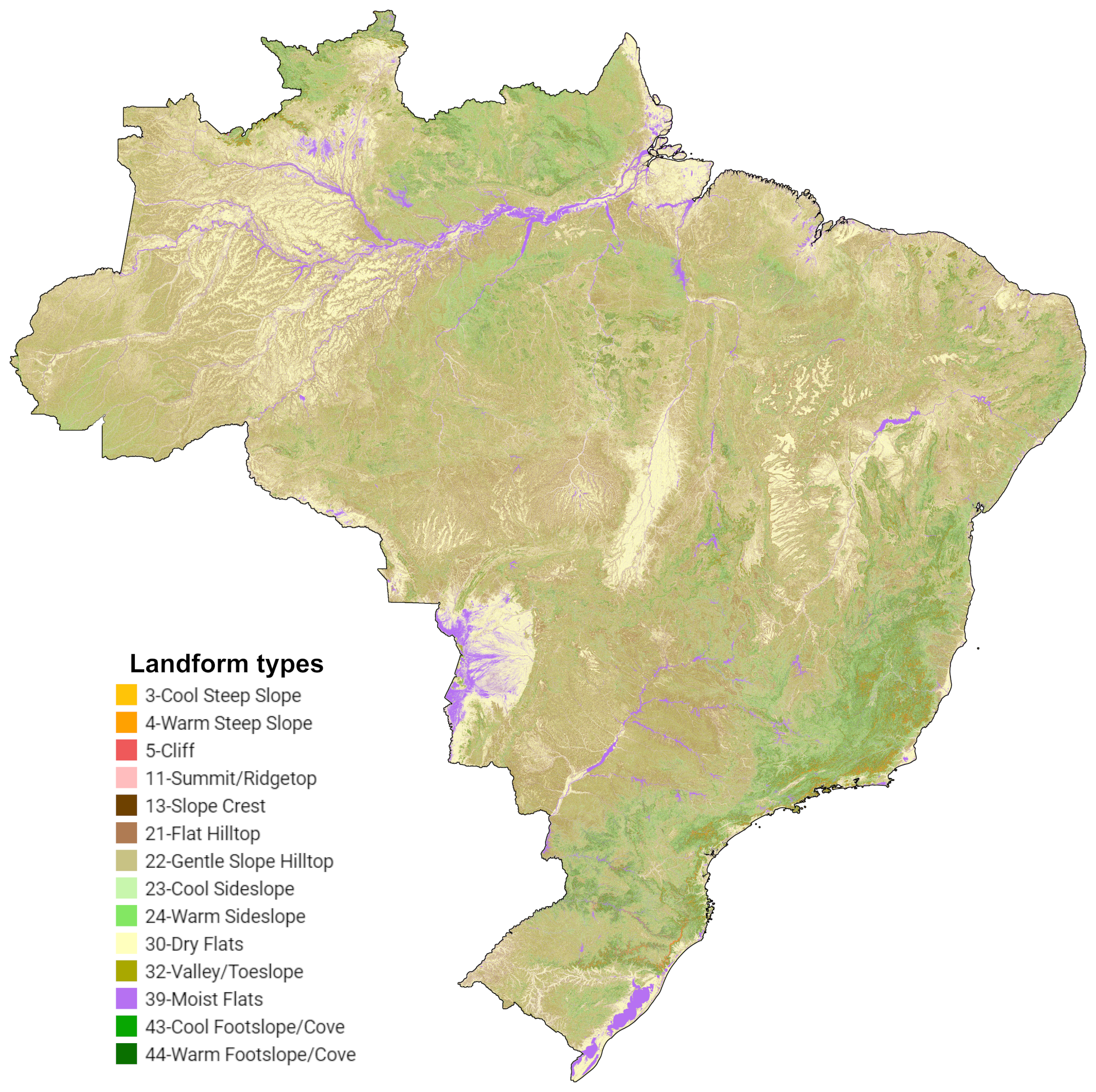
Exemplos de formas de relevo identificadas nos diferentes biomas do Brasil podem ser visualizados na Figura 11.3.
Obtendo a variedade de formas de relevo
A variedade de formas de relevo foi calculada como a quantidade de formas de relevo dentro de uma janela circular da célula focal. O tamanho do raio da janela foi definido calculando a variedade em diferentes raios (2, 5, 7, 10, 15 e 20 células) e calculando a diferença na média de variedade obtido para o Brasil a cada aumento de raio. O raio escolhido foi aquele em que o seu subsequente não adicionou variedade. Desta forma, o raio representa o nível de resolução da paisagem que captura o máximo de variedade de formas de relevo, sendo escolhido o valor de 5 células de raio (450 m) para todo o Brasil.
Em seguida, os valores de variedade de formas de relevo foram padronizados para posteriormente comporem a heterogeneidade da paisagem. A padronização utilizou uma janela móvel com 200 pixels de raio, onde calculamos a média da vizinhança (\(\mu\)) do valor da célula (\(X_{célula}\)) e o desvio padrão da vizinhança (\(\sigma\)). O valor de Z foi calculado subtraindo os valores das células pela média da sua vizinhança e dividindo pelo desvio padrão:
\[ Z_{célula}= \frac{X_{célula}-\mu_{vizinhança}} {\sigma_{vizinhança}} \]
Amplitude altitudinal
A amplitude altitudinal representa a variação da altitude em uma região, independente da variedade de formas de relevo. A amplitude altitudinal foi calculada como a diferença entre os valores máximos e mínimos de altitude, dentro de uma janela circular de 450 m (5 células de raio), a partir do MERIT-DEM (Yamazaki et al., 2017). Em seguida, fizemos uma Regressão Linear Simples (Ordinary Linear Regression) entre os valores de amplitude altitudinal e a variedade formas de relevo e obtivemos os valores dos resíduos dessa análise como a amplitude altitudinal independente da variedade de formas de relevo. Os valores de amplitude altitudinal foram também padronizados em valores de Z.
Índice de áreas úmidas
O índice de áreas úmidas foi calculado a partir dos dados da Global Wetlands Database (Gumbricht et al., 2017). Essa base de dados fornece informação e inventário de áreas úmidas para todo o mundo. Os dados são obtidos através de imagens de satélite, amostragens aéreas e relatórios publicados.
No presente estudo, reamostramos o mapa de áreas úmidas para a mesma resolução das demais variáveis. Depois, calculamos o índice de áreas úmidas considerando a densidade de áreas úmidas na escala local (450 m) e na escala regional (1170 m). Também foi incluído no índice final a quantidade de áreas úmidas regional (Anderson et al., 2016), conforme descrito a seguir.
Primeiro, calculamos a quantidade de áreas úmidas como o número de células de áreas úmidas dentro de uma janela local (450 m) e regional (1170 m). A divisão da quantidade de áreas úmidas pelo número de células na janela produz a densidade de áreas úmidas. Em seguida, as densidades de áreas úmidas local e regional e a quantidade de áreas úmidas regional foram transformados em valores de Z. A média e desvio padrão foram calculados dentro de uma vizinhança circular de 200 células de raio de cada célula focal. O índice de áreas úmidas foi calculado como a média ponderada da densidade local e regional, atribuindo peso 2 para a densidade local:
\[ Z_{índice\,de\,áreas\,úmidas}=\frac {{{(Z_{local}}{\times2)}}+{Z_{regional}}}{3} \]
Nos locais onde a quantidade de áreas úmidas regionais (valor de Z) eram maiores que o índice de áreas úmidas, o índice foi calculado como a média ponderada das densidades e da quantidade de áreas úmidas, conforme indicado a seguir:
\[ Z_{índice\,de\,áreas\,úmidas} =\frac {{{(Z_{local}}{\times2)}} + {Z_{regional}} + {Z_{quantidade}}}{4} \]
Riqueza de solos
A riqueza de solos foi calculada como a quantidade de tipos de solos dominantes e subdominantes nos polígonos de solo obtidos da base do Instituto Brasileiro de Geografica e Estatística (IBGE) (https://www.ibge.gov.br/geociencias/informacoes-ambientais/pedologia/10871-pedologia.html). Essa informação foi rasterizada e projetada na mesma resolução espacial das variáveis descritas anteriormente. Em seguida padronizamos a riqueza de solos em valores de Z utilizando a mesma metodologia descrita para as outras variáveis.
Calculando a heterogeneidade da paisagem
A heterogeneidade da paisagem (Figura 11.4) foi calculada seguindo uma hierarquia nas variáveis padronizadas por valores de Z na janela móvel. Na etapa 1, ela foi definida como o valor de Z da variedade de formas de relevo. Na etapa 2, em locais onde o valor de Z para amplitude altitudinal foi maior que aquele obtido para a variedade de formas de relevo, a heterogeneidade da paisagem foi calculada como a média ponderada das duas variáveis, dando peso 2 para variedade de formas de relevo:
\[ Z_{heterogeneidade\, da\,paisagem}= \frac{\left(Z_{formas\,de\,relevo}\times 2 \right)+Z_{amplitude\,altitudinal}}{3} \]
Na etapa 3, em locais onde o índice áreas úmidas foi maior que a heterogeneidade da paisagem calculada na etapa 2, calculamos a média ponderada da heterogeneidade da paisagem e índice de áreas úmidas, atribuindo peso dois para as áreas úmidas (conforme indicado abaixo). O peso duplo das áreas úmidas é justificado por esses locais estarem em áreas planas com baixa variabilidade topográfica, sendo as áreas úmidas locais com alta disponibilidade hídrica as que determinam a variabilidade microclimática.
\[ Z_{heterogeneidade\, da\,paisagem}= \frac{Z_{formas\,de\,relevo}+Z_{amplitude\,altitudinal} + (Z_{áreas\,úmidas}\times 2)}{4} \]
Se, na etapa 2, a amplitude altitudinal não foi importante para a célula, a heterogeneidade da etapa 3 foi calculada conforme segue:
\[ Z_{heterogeneidade\, da\,paisagem}= \frac{Z_{formas\,de\,relevo} + (Z_{áreas\,úmidas}\times 2)}{3} \]
Na etapa 4, nos locais onde o valor de Z da riqueza de solos foi maior que a heterogeneidade da paisagem calculada na etapa 3, os valores foram substituídos pela média ponderada das variáveis naquela localidade, com peso 2 para variedade de formas de relevo.
\[ Z_{heterogeneidade\, da\,paisagem}= \frac{(Z_{formas\,de\,relevo}\times 2)+Z_{amplitude\,altitudinal}+Z_{áreas\,úmidas}+Z_{riqueza\,de\,solos}}{5} \]
Se, na etapa 3, nas células onde o índice de áreas úmidas não foi importante, a heterogeneidade da paisagem foi calculada conforme segue:
\[ Z_{heterogeneidade\, da\,paisagem}= \frac{(Z_{formas\,de\,relevo}\times 2)+Z_{amplitude\,altitudinal}+Z_{riqueza\,de\,solos}}{4} \]
Da mesma forma, em locais onde a amplitude altitudinal não foi importante, a heterogeneidade da paisagem foi calculada conforme segue:
\[ Z_{heterogeneidade\, da\,paisagem}= \frac{(Z_{variedade\,de\,formas\,de\,relevo}\times 2)+Z_{índice\,de\,áreas\,úmidas}+Z_{riqueza\,de\,solos}}{4} \]
Por fim, em locais onde apenas a variedade de formas de relevo foi importante até aqui, a heterogeneidade da paisagem foi calculada conforme segue:
\[ Z_{heterogeneidade\, da\,paisagem}= \frac{(Z_{variedade\,de\,formas\,de\,relevo}\times 2) + Z_{riqueza\,de\,solos}}{3} \]